Grundlagen der Farbmesstechnik

Bei Projektoren und Displays wird von Seiten der Hersteller die Lichtleistung bzw. die Helligkeit des erzeugten Bildes oft als wichtiges Produktmerkmal herausgestellt. Die maximale Bildhelligkeit liefert dem Anwender eine Information darüber, für welche Anwendungen und unter welchen Umgebungslichtbedingungen das betreffende Gerät mit gutem Ergebnis einsetzbar ist. Entsprechend werden in unseren Tests die entsprechenden Herstellerangaben überprüft. Etwas schwieriger vermittelbar sind die Farbwiedergabequalitäten eines Präsentationsgerätes, da sie sich nicht so einfach auf einen einzelnen Zahlenwert reduzieren lassen. In der Produktliteratur liest man z.B. von „hoher Farbbrillianz“ oder in den technischen Daten davon, daß das betreffende Gerät über 16 Millionen Farben darstellen kann. Ob dies unmittelbar mit einer subjektiv guten bzw. naturgetreuen Farbwiedergabe zusammenhängt, ist damit jedoch nicht gesagt.
Farbe ist eigentlich keine direkt physikalisch meßbare Größe, sondern ein Merkmal, das von der menschlichen Wahrnehmung erzeugt wird. Allerdings hängt die Wahrnehmung von Farben mit den physikalischen Eigenschaften des Lichts bzw. der Objekte zusammen, die als farbig wahrgenommen werden. Das liegt daran, dass es in der Netzhaut des Auges drei verschiedene Sorten von farbempfindlichen Sinneszellen gibt, die sog. Stäbchen, die sich hinsichtlich ihrer spektralen Empfindlichkeit unterscheiden. Sie reagieren also in Abhängigkeit von der Wellenlänge des Lichts in unterschiedlicher Weise.
Da es nur drei verschiedene Arten von farbempfindlichen Rezeptoren (Sinneszellen) in der Netzhaut gibt, kann man im Prinzip alle Farbwahrnehmungen erzeugen, indem man die Sinneszellen passend zur jeweiligen Farbe anregt. Das kann man zum Beispiel dadurch tun, daß man drei Grund-Lichtfarben (Primärfarben, z.B. rot, grün, blau) benutzt, die die Sinneszellen jeweils unterschiedlich stark reizen. Diese drei Grundfarben sind dabei zunächst nicht festgelegt.
In welchem Anteil man diese Primärfarben mischen muß, um einen bestimmten Farbeindruck zu erzielen, kann man in einem Experiment ermitteln, in dem man Versuchspersonen bittet, den Anteil der drei Grundfarben so zu verändern, daß die resultierende Farbe einem gleichzeitig gesehenen Vergleichs-Farbmuster entspricht.
Interessant ist bei diesem Experiment, dass die spektrale Verteilung des Vergleichsmusters im allgemeinen nicht gleich derjenigen des von der Versuchsperson aus den drei Grundfarben gemischten Lichtes ist – lediglich die Anregung der Sinneszellen im Auge stimmt überein.
Dieser Tatsache verdanken sämtliche Farbdisplays, der Farbfilm und auch der farbige Druck ihre Existenz: Um eine Farbe nachzubilden, muß nicht das gesamte Spektrum identisch sein, es genügt, mit (mindestens) drei Grundfarben die Sinneszellen in gleicher Weise anzuregen.

Nimmt man als Vergleichsmuster in dem zuvor erwähnten Experiment reine Spektralfarben (die etwa durch ein Prisma aus weißem Licht erzeugt werden), kann man bestimmen, in welchen Anteilen die (zunächst willkürlich gewählten) Grundfarben (die sog. Primärvalenzen) gemischt werden müssen, um denselben Farbeindruck wie die Spektralfarben zu erzeugen.
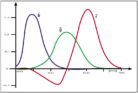
Trägt man diese Ergebnisse in ein Diagramm ein, so erhält man die sogenannten Spekralwertfunktionen für die drei benutzten Grundfarben. Nimmt man z.B. die reinen Spektralfarben Rot (700nm), Grün (546,1nm) und Blau (435,8nm) als Grundfarben, so ergeben sich die in Abb.1 dargestellten Spektralwertfunktionen.
Mit Hilfe dieser Spektralwertfunktionen läßt sich also jede sichtbare Farbe durch die Angabe der drei Anteile (bzw. Teilhelligkeiten) der gewählten Grundfarben (hier Rot, Grün und Blau) eindeutig beschreiben. Anders ausgedrückt: Wenn man die Teilhelligkeiten der drei Grundfarben als Koordinaten in einem dreidimenisonalen, rechtwinkligen Koordinatensystem benutzt, so läßt sich jede Farbe als Ortsangabe (Farbort) eines Punktes in einem dreidimensionalen (Farb-)Raum darstellen.
Das Ergebnis für diesen RGB-Farbraum wirkt nur insofern etwas merkwürdig, als dass die Spektralwertfunktion für Rot auch negativ wird, was eigentlich einer negativen Helligkeit entspräche. Des Rätsels Lösung besteht darin, dass im o.g. Farbmischexperiment für spektral reine Testfarben zwischen etwa 440nm und 650nm durch die Mischung der drei Grundfarben allein keine Übereinstimmung zu erzielen ist. Das gelingt erst, wenn der Rotanteil nicht der Mischfarbe, sondern der Referenzfarbe zugegeben wird und dadurch quasi mit umgekehrtem Vorzeichen in Erscheinung tritt.
Nebenbei bemerkt bedeutet das auch, daß ein technisches Display mit den Grundfarben Rot, Grün und Blau nicht alle für den Menschen wahrnehmbaren Farben darstellen kann. Aber dazu später mehr.
Diesen Nachteil – der auch die technischen Realisierbarkeit von Farbmeßgeräten erschwert – kann man vermeiden, wenn man etwas andere Grundfarben wählt. Die Farbwahrnehmung hängt ja – wie eingangs beschrieben – nicht von der Wahl des Koordinatensystems bzw. der Grundfarben ab. Also kann man sich auch andere Grundfarben aussuchen, die einem besser passen.
Dazu braucht man nicht mühselig auf die Suche nach neuen Farben zu gehen, sondern kann das rein mathematisch durch eine Koordinatentransformation erledigen. Bei dieser Gelegenheit kann man das Koordinatensystem auch gleich so anlegen, daß es einige (auch für messtechnische Zwecke) gewünschte Eigenschaften hat:
1. Die Werte der neuen Spektralwertfunktionen sollen für alle sichtbaren Farben ausschließlich positive Zahlenwerte haben.
2. Diese Zahlenwerte sollen zwischen 0 und 1 liegen.
3. Der durch alle damit darstellbaren Farben entstehende dreidimensionale Farbkörper soll den verfügbaren Wertebereich möglichst gut ausfüllen.
4. Eine der Spektralwertfunktionen soll der Hellempfindlichkeitskurve des Auges entsprechen. Das heißt: Aus der Spektralwertfunktion einer der neuen Grundfarben soll man gleichzeitig ein Maß für die subjektiv empfundene Helligkeit berechnen können.
5. Für Licht mit konstanter spektraler Leistungsdichte sollen die neuen Farbkoordinaten X, Y und Z gleich sein.
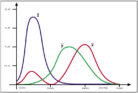
Durch diese hier beschriebene Koordinatentransformation erhält man die neuen, virtuellen Grundfarben X,Y, und Z. Sie sind rein mathematische Konstrukte, deutlich gesättigter als reine Spektralfarben und daher nicht mehr direkt herstellbar oder sichtbar.

Die zugehörigen Spektralwertfunktionen sind in Abb. 2 dargestellt. Sie weisen keine negativen Werte mehr auf. Der Koordinatenwert von Y entspricht dabei der Helligkeit.
Auch in diesem neuen XYZ-Farbraum werden Farben als Punkte in einem dreidimensionalen Raum beschrieben. Die virtuellen Farben X, Y und Z sind nicht mehr real als farbiges Licht herstellbar, weil sie gesättigter sein müssten als reine Spektralfarben. Man kann sie zwar nicht herstellen oder sehen, aber trotzdem ganz einfach ihre jeweiligen Helligkeitsanteile an einer beliebigen Testfarbe messen bzw. berechnen.
Ihre Anteile bzw. Koordinaten x(λ), y(λ) und z(λ) werden berechnet, indem man das Spektrum des Lichtes der Testfarbe mit den neuen Spektralwertfunktionen gewichtet (multipliziert) und das Ergebnis über den Wellenlängenbereich des sichtbaren Lichtes integriert.
Diese Gewichtung mit den Spektralwertfunktionen kann man entweder rechnerisch machen – dann muss man zuerst das Lichtspektrum der Testfarbe messen und dann die Berechnung durchführen. Man kann aber auch vor einen Photosensor einen Farbfilter schalten, dessen wellenlängenabhängige Durchlasscharakteristik genau einer der drei Spektralwertfunktionen entspricht. Dann passiert die Gewichtung und die Integration quasi automatisch, und das Ausgangssignal des Lichtsensors ist direkt proportional zu der Farbkoordinate X, Y oder Z, je nachdem welcher Filter sich vor dem Photosensor befindet.
Eine ganze Reihe Messgeräte funktioniert genau so, dass das zu messende Licht von drei möglichst präzisen optischen Filtern gefiltert und dann von Photodioden erfasst wird. Die nachfolgende Elektronik berechnet aus den Ausgangssignalen der Photosensoren letztendlich die gewünschten Farbkoordinaten.
Die Präzision steht und fällt bei solchen Messgeräten mit der Qualität der Filter. Abweichungen in der Filterfunktion schlagen direkt als Messfehler zu Buche. Das ist besonders dann problematisch, wenn man es mit schmalbandigen Lichtquellen zu tun hat, die ihr Licht auf einer Wellenlänge aussenden, bei welcher der jeweilige Filter gerade produktionsbedingt eine größere Abweichung von der „wahren“ Spektralwertfunktion hat. Da die Spektralwertfunktion x(λ) zwei Maxima hat, muss man hier technisch eigentlich mit zwei Filtern und Fotodioden arbeiten, was natürlich den Aufwand erhöht. Daher macht man sich gern die Ähnlichkeit des kurzwelligen Anteils von x(λ) mit der Form von z(λ) zunutze und ersetzt x1(λ) durch eine skalierte Version von z(λ), indem man das Meßsignal für Z mit einem Korrekturfaktor dem X-Signal zumischt. Da die Formen der beiden Kurven nicht hundertprozentig identisch sind, bleibt auch hier ein Rest-Messfehler.
Deswegen und wegen der, bei bezahlbaren Preisen, begrenzten Filtergenauigkeit empfehlen die Hersteller solcher Dreifilter-Messgeräte normalerweise für breitbandige Lichtquellen wie etwa Glühlampenlicht. Soll es genauer sein, etwa für Messungen an LEDs oder Lasern, muss man zunächst das Spektrum des zu messenden Lichtes ermitteln und kann dann ohne weitere Fehler die Farbkoordinaten durch reine Rechenoperationen bestimmen. Auch spektrometerbasierte Farbmessgeräte sind natürlich nicht fehlerfrei – die Fehlerquelle liegt hier dann eher bei der Präzision der Messung des Spektrums. Generell sind solche spektrometerbasierten Messgeräte bei schmalbändigen Lichtquellen aber deutlich genauer als filterbasierten – in der Regel leider auch teurer.
Farbdiagramme
Um Farben auch in zweidimensionalen Grafiken anschaulich darstellen zu können, macht man sich die Tatsache zunutze, daß die neue Koordinate Y allein schon die Helligkeit komplett beschreibt und trennt daher die Helligkeit Y der Farbe von ihrem Farbton.
Um den Farbton grafisch darstellen zu können, wendet man wieder einen kleinen mathematischen Trick an. Man arbeitet mit normierten Farbwerten x, y und z, die durch einen Normierungsfaktor 1/(X+Y+Z) aus den Farbkoordinaten X, Y, und Z berechnet werden. Da durch diese Normierung immer x+y+z=1 gilt, kann man immer einen dieser drei Werte aus den beiden anderen berechnen und braucht deshalb nicht mehr drei, sondern nur noch zwei Koordinaten, um den Farbton einer Farbe grafisch darzustellen.
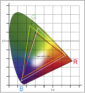
Normalerweise nimmt man für die Darstellung die Koordinaten x und y, so daß sich eine Farbe durch die Angabe der Helligkeit Y und die Farbortkoordinaten x und y vollständig beschreiben läßt. Der so entstehende Farbraum wurde bereits im Jahre 1931 von der Commision International d’Eclairage (CIE) genormt und ist daher auch als CIE-Yxy-Farbraum bekannt.
Eine grafische Darstellung der sichtbaren Farben in diesem CIE-Yxy-Farbraum ist auch als Normfarbtafel bekannt. Die sehr charakteristische Form, die an ein Hufeisen bzw. an einen liegenden Zuckerhut erinnert, hat ihren Ursprung letztendlich in der Form der Spektralwertfunktionen, wie sie im eingangs beschriebenen Farbmisch-Wahrnehmungsexperiment bestimmt wurden.
Dabei liegen alle spektral reinen Farben auf dem gekrümmten Rand der Grafik. Die beiden Enden werden durch eine Gerade verbunden, auf der alle Purpurtöne, also Mischfarben aus spektral reinem Rot und Blau, liegen. Der Farbort für Licht mit konstanter spektraler Leistungsdichte liegt per Definition des XYZ-Koordinatensystems bei [x=0,33; y=0,33], dem sogenannten Unbuntpunkt. Normalerweise nimmt man als weißes Licht allerdings das Licht eines Temperaturstrahlers (Hohlraumstrahler, Glühlampe) mit definierter Temperatur. Dies wird normalerweise entsprechend gekennzeichnet, so hat der Weißpunkt D65 für Licht der Farbtemperatur 6500 Kelvin die Farbortkoordinaten x=0.3127, y=0.3290.
In dieses zweidimensionale xy-Farbdiagramm (siehe Einleitungsbild dieses Artikels) kann man nun die Farbtöne aller sichtbaren Farben eintragen, so zum Beispiel die von der CIE ebenfalls genormten Grundfarben Rot, Grün und Blau des CIE-RGB-Farbraums. Die Grundfarben sind ja eigentlich willkürlich, diese hier sind Spektralfarben, deren Farbe sich aus Gründen der praktischen Herstellbarkeit zum Teil (Grün, Blau) an den Spektrallinien einer Quecksilberdampflampe orientieren. Die Farborte dieser (CIE-)Grundfarben R, G und B spannen ein Dreieck im CIE-Yxy-Farbraum auf.
Farben, die mit additiver Farbmischung aus zwei dieser Grundfarben gebildet werden, liegen auf der Verbindungslinie zwischen diesen Grundfarben. Alle Mischfarben, die aus Kombinationen von R, G und B gebildet werden können, liegen daher innerhalb des von R, G und B aufgespannten Dreiecks. Alle Farben, deren Farborte auf der Verbindungslinie zwischen (irgend)einer Referenzfarbe und dem (aktuell verwendeten) Weißpunkt liegen, haben denselben Farbton wie diese, aber eine zum Weißpunkt hin abfallende Farbsättigung.
Farben, die im CIE-Yxy-Diagramm außerhalb des RGB-Dreiecks liegen, können nicht durch additive Farbmischung aus den drei Grundfarben Rot, Grün und Blau gebildet werden.
Dieser letzte Aspekt ist für technische Anwendungen von großer Bedeutung: Um eine möglichst große Farbvielfalt darstellen zu können, müssen die Grundfarben möglichst stark gesättigt sein, also möglichst weit außen im CIE-Yxy-Farbdiagramm liegen, damit der Farbraum, innerhalb dessen Mischfarben gebildet werden können, möglichst groß ist.
Die Anzahl der darstellbaren Farben hat damit nur mittelbar etwas zu tun. Auch bei einer Auflösung von 256-Helligkeitsabstufungen (8Bit) pro Grundfarbe (entsprechend 256*256*256= 16,78 Mio. Farbstufungen) kann man zwar entsprechend viele Zustände des Ausgabegerätes erzeugen.
Alle so entstehenden Mischfarben können aber trotzdem nur innerhalb des von den Grundfarben aufgespannten Dreiecks liegen. Wenn dieses Dreieck klein ist, haben selbst die Grundfarben nur eine geringe Farbsättigung. Demzufolge ist auch nur ein geringerer Teil der insgesamt wahrnehmbaren Farben auf dem Display darstellbar – trotz der großen Anzahl von Farbabstufungen, die das menschliche Auge dann ggf. gar nicht mehr alle unterscheiden kann.
Wichtig ist in diesem Zusammenhang auch, daß Farben, die im RGB-Farbmodell – also z.B. auf Computern – definiert werden, auf verschiedenen Präsentationsgeräten unterschiedlich aussehen können. In aller Regel sind die Grundfarben R, G und B in Präsentationsgeräten keine reinen Spektralfarben, sondern werden bei Projektoren durch Lampenspektrum und Filterfarben, bei LCD-Bildschirmen durch die Farbe des Backlights und der Farbfilter und bei bei OLED-Monitoren durch die Farbe der zum Leuchten angeregten organischen Substanzen bestimmt. Eine Mischfarbe aus z.B. 100% Rot und 100% Grün kann daher im CIE-Yxy-Farbdiagramm an unterschiedlichen Farborten liegen, je nachdem, wo sich für das jeweilige Display die Farborte von dessen Grundfarben R und G befinden.
Bei Präsentationen mit Geschäftsgrafiken ist das meist weniger schlimm – hier freut man sich vielleicht sogar über ggf. stärker gesättigte Farben. Bei Fotos und Videos kann das schon ganz anders aussehen, denn es ist keineswegs sicher, daß die Grundfarben bei verschiedenen Ausgabegeräten sich nur in der Farbsättigung unterscheiden, aber identische Farbtöne haben.
Wenn man Pech hat, ist das nicht der Fall – und dann gibt es Verschiebungen bei allen Farbtönen, was z.B. bei Hauttönen schnell unnatürlich aussehen kann.
Aus diesem Grund gibt es nicht nur verschiedene Methoden zur Farbkalibrierung von Ausgabegeräten, sondern für verschiedene Anwendungen auch Vereinbarungen über den zugrundeliegenden Farbraum.
So gibt es z.B. Farbraumstandards für verschiedene Fernsehnormen (z.B. für PAL / ITU-R709 die Grundfarben R: [0,6400; 0,3300], G: [0,2900; 0,6000], B: [0,1500; 0,0600], Weißpunkt (D65): [0,3127; 0,3290]) oder das in Computerkreisen verbreitete sRGB.
Die Primärfarben des sRGB-Farbraums entspricht denen des PAL-Farbraums, dieser ist also deutlich kleiner als der CIE-RGB-Farbraum, der mit reinen Spektralfarben aufgespannt wird. Neben TV-Monitoren arbeiten auch aktuelle Computermonitore meist mit dem sRGB-Farbraum, so daß man auch ohne ausdrückliche Farbkalibrierung eine gute Chance hat, Fotos und Videoeinspielungen ohne wesentliche Farbverschiebungen wiedergeben zu können.
Nun kann es durchaus sein, daß Projektoren und Displays aufgrund ihrer Farberzeugung mit einem größeren Farbraum als sRGB arbeiten, die Farben also gesättigter sein können, als z.B. auf dem Computermonitor. Das ist für sich genommen nichts Schlechtes, zu Problemen kann es allerdings kommen, wenn Content, der für einen bestimmten Farbraum erstellt wurde, mit einem Wiedergabegerät angesehen wird, das mit einem anderen Farbraum arbeitet.
In diesem Fall werden alle Farbtöne verschoben, was normalerweise unerwünscht ist.
Es ist also interessant zu wissen, ob die in einem Wiedergabegerät jeweils verwendeten Grundfarben auch hinsichtlich ihres Farbtons vom Zielfarbraum, z.B. sRGB, abweichen. Um das herauszufinden, muß man die Farborte der Primärvalenzen (Grundfarben) messen und überprüfen, ob deren Farbton sowie der Weißpunkt mit einem Standard (z.B. sRGB) übereinstimmt. Dies ist dann eine Voraussetzung dafür, dass keine Verschiebungen bei der Wiedergabe von Farbtönen auftreten.
Die erforderliche Messung ist relativ einfach und erfolgt mit einem Colorimeter. Viele professionelle Anwender, etwa Vermietfirmen für Projektoren, setzen dafür die besagten Dreifiltergeräte ein. In modernen Präsentationsgeräten kommen aber zunehmend auch Halbleiterlichtquellen zum Einsatz, die zum Teil relativ schmalbandig arbeiten – so etwa in den aktuellen Laser-Phosphor-Projektoren. Einfache Colorimeter produzieren bei solchen Geräten Messfehler, weshalb man für diesen Zweck Farbmessgeräte einsetzen sollte, die auf der Basis einer Spektralanalyse arbeiten und daher wesentlich genauere Ergebnisse liefern.
Gefällt dir der Artikel?
Dann teile ihn mit deinen Freunden.
Benutze dafür unsere Links: